Vito M. R. Muggeo – Università degli studi di Palermo
Andrea Consiglio – Università degli studi di Palermo
Gianluca Sottile – Università degli studi di Palermo
Vincenzo G. Genova – Università degli studi di Palermo
Giorgio Bertolazzi – Università degli studi di Palermo
Mariano Porcu – Università di Cagliari
In questo contributo vogliamo discutere di un modello di regressione segmented per valutare e quantificare l’effetto delle misure di contenimento individuando gli istanti temporali in cui la diffusione della malattia rallenta.
Introduzione
Il 9 gennaio 2020 l’Organizzazione Mondiale della Sanità (OMS) ha diffuso la notizia che le autorità sanitarie cinesi avevano individuato un nuovo ceppo di virus mai identificato prima nell’uomo. Il nuovo virus è stato provvisoriamente denominato “2019-nCoV” ed è stato poi classificato con il nome di “SARS-CoV-2”. L’11 febbraio 2020 l’OMS ha classificato la malattia respiratoria determinata dal nuovo virus usando la denominazione COVID-19. Da allora, discussioni sulla curva dei contagi, analisi e possibili “previsioni” sono diventate ricorrenti. La curva dei contagi è la rappresentazione grafica di un modello[1] teorico largamente impiegato per descrivere la crescita delle popolazioni. Il modello di riferimento in letteratura prende il nome di modello logistico [1] e la sua rappresentazione è una curva liscia che ha la forma di una “S” allungata. In breve, il modello descrive la dinamica del numero dei contagiati che cresce dapprima lentamente, poi molto velocemente (crescita esponenziale), raggiunge un determinato istante e continua a crescere sempre più lentamente fino ad arrestarsi. Questo istante che d’ora in poi indicheremo con , indica, quindi, un rallentamento della diffusione del virus. In altre parole, quella corsa verso l’alto dei contagi che appare inarrestabile durante le prime fasi dell’epidemia e poi rallenta a ridosso di un tempo che segna, quindi, il momento in cui le armi contro la diffusione della malattia iniziano a vincere. Capire, quindi, quando la curva di crescita si sta avvicinando a ha un’importanza fondamentale e soprattutto è importante riuscire a cogliere i più impercettibili segnali di variazione dell’andamento esponenziale che preannunciano l’arrivo del punto . Questi cambiamenti, anche se contenuti, possono avere importanti effetti sulle politiche sanitarie di gestione delle cure, permettendo al sistema sanitario di combattere la malattia e di circoscrivere la sua diffusione, nonché di guadagnare tempo prezioso necessario a trovare un vaccino o cure efficaci e accessibili per contrastare gli effetti dell’infezione. Ma i segnali che “annunciano” questo punto di cambio , ovvero possibili rallentamenti nella crescita dell’epidemia sono importanti anche per comunicare con l’opinione pubblica. Infatti, secondo i dati attualmente disponibili[2] il contagio da persona a persona di COVID-19 è la causa più frequente di diffusione della malattia e la riduzione dei contatti sociali è, quindi, l’arma al momento più importante per contrastare la diffusione della malattia.
In questo contributo vogliamo discutere di un metodo statistico per valutare e quantificare l’effetto delle misure di contenimento individuando gli istanti temporali in cui la diffusione della malattia rallenta. Di seguito, presenteremo dapprima il modello, poi i risultati ottenuti dell’applicazione sui dati reali.
Il modello
Sia Ct il numero di casi totali al giorno t. Ct potrebbe essere un qualsiasi altro dato, come il numero di attualmente positivi o decessi. Il numero totale dei casi viene qui inteso come un indicatore dell’impatto dell’epidemia sul sistema sanitario. Nella sezione precedente si è visto che l’evoluzione naturale di una malattia può essere rappresentato da una funzione logistica, che nella sua fase iniziale ha andamento esponenziale. Quindi se indichiamo con E[Ct] = μt il numero medio di conteggi al giorno t, si ha che:
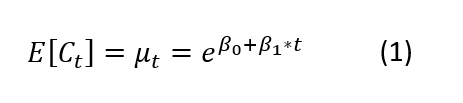
Dove E[Ct] è il valore atteso del numero dei contagi e β1 misura la pendenza della retta di regressione su scala logaritmica. In maniera equivalente, si può esprimere il tasso di crescita e β1 – 1 come variazione media relativa tra il giorno t e il successivo. Si osservi che, l’evolversi naturale dell’epidemia potrà essere modificato da “fattori esterni” come le misure di distanziamento sociale, che avranno l’effetto di trasformare la (1) come segue:
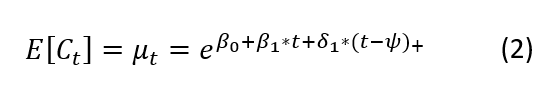
Il termine aggiuntivo δ1 * (t – ψ)+ fornisce la correzione all’andamento medio generale di Ct , e ψ è l’istante di tempo in cui avviene il cambio di regime. In tal modo, nel caso in cui i fattori esterni non avessero alcun impatto, il tasso di crescita si manterrebbe pari a e β1 – 1.
Nel caso in cui al tempo ψ si verificasse un punto di svolta, il nuovo tasso di crescita sarebbe e β1 + δ1 – 1.
Si osservi che, valori di δ1 < 0 implicano una riduzione del tasso di crescita a partire dall’istante ψ che, nel contesto epidemico, indica un rallentamento della diffusione della malattia, ragionevolmente, nel caso del COVID-19 attribuibile alle misure di distanziamento sociale.
I parametri dell’equazione (2) relativi anche ad eventuali termini aggiuntivi che esprimono diversi cambi di regime sono stimati congiuntamente mediante una funzione di verosimiglianza assumendo che i conteggi seguano una distribuzione di Poisson. I risultati e i grafici sono prodotti attraverso il pacchetto “segmented” [2,3] implementato in ambiente R.
Il modello di regressione segmented per l’analisi dell’epidemia di COVID19 è stato discusso in [4]. Il gruppo di ricerca CoViSTAT19 ha effettuato il monitoraggio giornaliero dell’epidemia a partire dal 20 marzo 2020 e i risultati delle analisi sono pubblicati sul sito https://unipa.it/covid19 .
Applicazione
L’analisi è stata condotta sui dati dei contagi relativi a diverse dimensioni territoriali: Italia, Italia Meridionale, Sicilia, Sardegna, Lombardia e Puglia. La stima dei modelli è avvenuta su base giornaliera e il criterio BIC ha guidato la scelta del numero di cambi di regime (breakpoints).
A titolo illustrativo, la Figura 1 mostra i risultati per la Lombardia per due istanti temporali di analisi: il 21/03 e il 25/03.
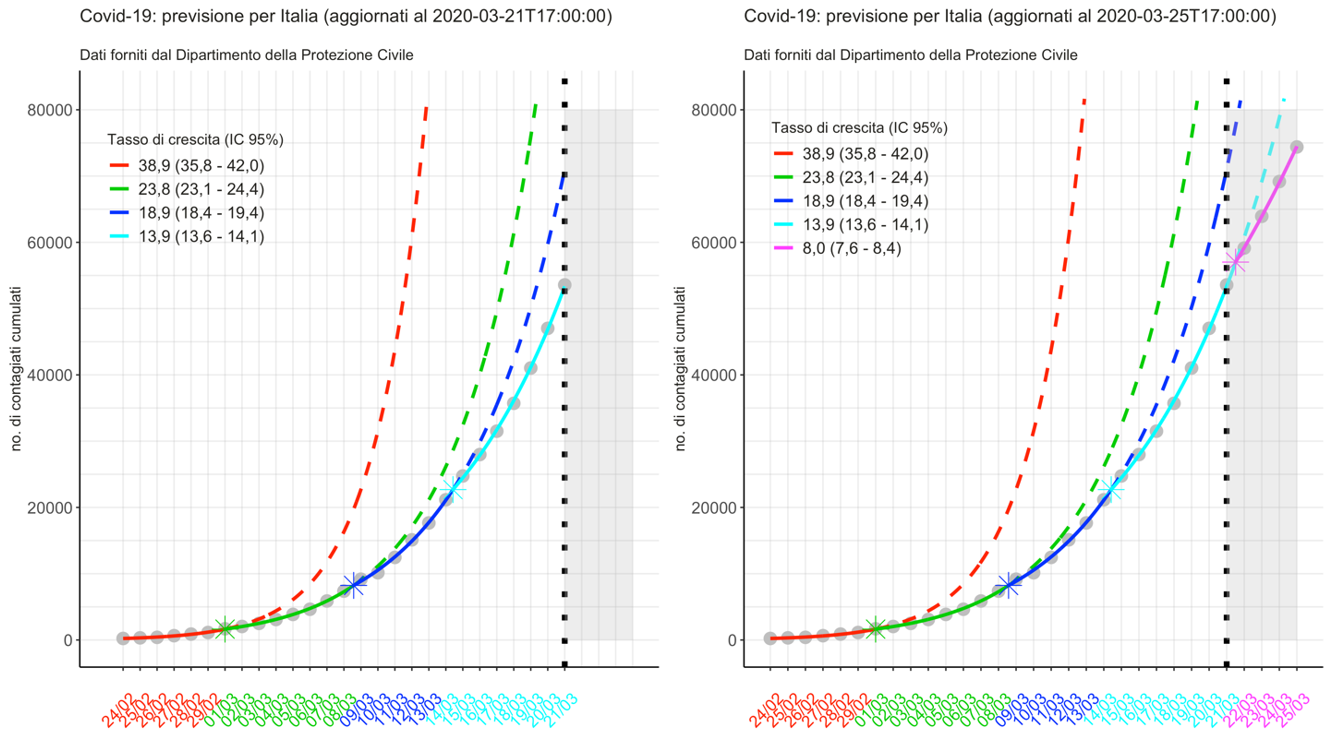
Figura 1: Analisi della serie giornaliere dei contagiati totali in Lombardia al 21/3 (grafico a sinistra) e al 25/03 (grafico a destra). I punti grigi rappresentano le osservazioni giornaliere, mentre le linee continue l’andamento stimato. Al 21/03 (grafico a sinistra) il modello aveva individuato 3 breakpoints, mentre dopo 4 giorni le nuove osservazioni sono state ‘classificate’ in un ulteriore regime di crescita con una leggera contrazione rispetto al precedente. I colori diversi identificano i diversi regimi di crescita esponenziali riportarti in legenda a sinistra, mentre le linee tratteggiate indicano il trend che si sarebbe osservato se non si fossero registrati i rallentamenti, stimati in corrispondenza del 29/2, 8/03, 13/03 e 21/03 e ragionevolmente attributi alle misure #iorestoacasa.
Al 21/03 la stima del tasso di crescita era pari al 13,9% con IC(95%) (13,6%-14,1%). Dopo 4 giorni di osservazioni, il modello ha individuato un nuovo breakpoint suggerendo una ulteriore riduzione del tasso di crescita fino al 8,0% con IC(95%) (7,6% – 8,4%).I quattro istanti temporali 29/02, 8/03, 13/03 e 21/03 stimati rappresentano i giorni in cui la crescita dell’epidemia ha subìto una contrazione. Ovvero pur rimanendo l’andamento di fondo a carattere esponenziale, i tassi di crescita sono progressivamente diminuiti.
La causa di rallentamenti stimati a partire dal secondo breakpoint (8 marzo) è verosimilmente da attribuirsi alle misure di contenimento #iorestoacasa che per la Lombardia sono state emanate con decreti che si sono susseguiti nei giorni: 25 febbraio (misure di contenimento in Lombardia), 4 marzo (Università e Scuole chiuse) e 11 marzo (misure di contenimento estese in tutta Italia). Invece, per quanto riguarda il primo breakpoint stimato il 29/2, la contrazione del tasso di crescita (dal 38,9% al 23,8%) potrebbe essere anche parzialmente attribuibile al cambio di politica nella somministrazione dei tamponi.
[1] Inteso come una riproduzione schematica e semplificata della realtà.
[2] http://www.salute.gov.it/portale/nuovocoronavirus/dettaglioContenutiNuovoCoronavirus.jsp?lingua=italiano&id=5337&area=nuovoCoronavirus&menu=vuoto
Riferimenti Bibliografici
- A.Tsoularis, J WALLACE (2002) Analysis of logistic growth models. Mathematical Biosciences, Volume 179, Issue 1, Pages 21-55
- Muggeo V.M.R.. Estimating regression models with unknown break‐points. Statistics in Medicine, 22, 3055-71, DOI: 10.1002/sim.1545, 2003.
- Muggeo, V. M. R.(2008) segmented: An R package to Fit Regression Models with Broken-Line Relationships ,R NEWS. 8/1, pag. 20-25.
- Muggeo V.M.R. e Porcu M.. La curva dei contagiati da COVID-19: la ricerca del punto di svolta, 2020 (https://www.neodemos.info/articoli/la-curva-dei-contagiati-da-covid-19-la-ricerca-del-punto-di-svolta/).