Laura Ventura
Walter Racugno [1]
Allo scopo di studiare l’evoluzione dei dati sui decessi e sui ricoveri in terapia intensiva forniti dalla Protezione Civile nel periodo 24 febbraio – 30 marzo 2020 è stato adottato un modello di regressione nonlineare. Questo tipo di modelli è spesso utilizzato per curve di crescita/decrescita in ambito farmacologico ed epidemiologico dove i parametri del modello forniscono interessanti interpretazioni per la comprensione della evoluzione del fenomeno in studio, quali ad esempio l’asintoto orizzontale e il punto di flesso.
Nel caso del Covid-19 i dati rilevati sono poco affidabili e le condizioni della loro rilevazione dipendono da molti fattori non sempre noti e per di più mutevoli nel corso della rilevazione stessa: si pensi alle concomitanti cause di decesso che possono variare da regione a regione in dipendenza della diversità delle misure restrittive e del rigore con cui queste sono rispettate o delle differenti capacità di accoglienza in terapia intensiva che varia da zona da zona. In tale contesto risulta appropriato ricorrere a procedure di analisi robuste. Dove la robustezza va intesa sia rispetto alle assunzioni del modello sia all’affidabilità dei dati.
Questi due diversi aspetti della robustezza, pur concettualmente distinti, sono tuttavia molto vicini tra loro e spesso equivalenti dal punto di vista del trattamento pratico.
Un approccio generale allo studio della robustezza, che unifica i due aspetti nella loro trattazione si basa sulla nozione di funzione di influenza (Huber e Ronchetti, 2009). In tempi relativamente recenti (Dawid et al. 2016) sono state proposte delle verosimiglianze surrogate (pseudo-verosimiglianze) date dalle cosiddette proper scoring rules. Si tratta di funzioni di perdita mediante le quali è possibile misurare la qualità di una distribuzione di probabilità per una variabile aleatoria di interesse, in vista della sua determinazione campionaria.
Per lo studio dei dati del Covid-19 ci siamo basati sul Tsallis score (Basu et al., 1998) che in generale fornisce procedure robuste ed è di facile applicazione per modelli di regressione nonlineare assumendo alternativamente come modello centrale la distribuzione normale o di Poisson o la Binomiale Negativa. L’estensione all’approccio bayesiano a partire da pseudo-verosimiglianze robuste (Ventura e Racugno, 2016), quale appunto la Tsallis scoring rule, risulta tanto più appropriato quanto più gli esperti di dominio (virologi, operatori sanitari, studiosi dei fenomeni epidemici in generale) possono aiutare nell’elicitazione delle prior.
Allo stato attuale delle analisi ci limitiamo all’uso di prior da default (Objective Bayesian Analysis), non disponendo ancora di informazioni sufficienti per elicitazioni soggettive.
Le applicazioni riguardano il numero cumulato dei decessi giornalieri e il numero dei ricoverati in terapia intensiva, regione per regione e totali nazionali.
A titolo di esempio sono riportati qui di seguito alcuni grafici descrittivi riguardanti i decessi e i pazienti in terapia intensiva a livello nazionale e, inoltre, le corrispondenti distribuzioni predittive di breve periodo e le distribuzioni a posteriori del punto di flesso in base ai dati disponibili al 30 marzo 2020.
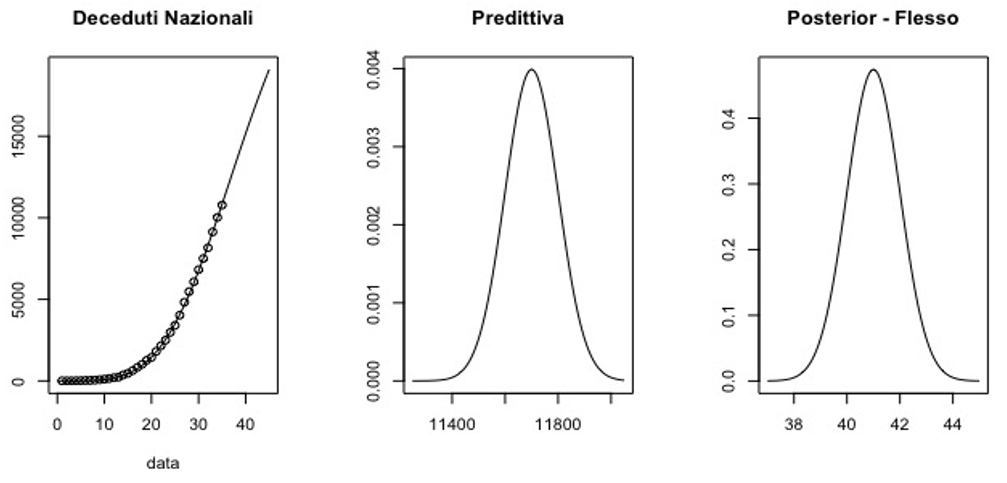
Figura 1: Decessi
I grafici rappresentano, nell’ordine: modello log-logistico stimato (linea) e i dati osservati (punti); distribuzione predittiva del numero di decessi al 30 marzo; distribuzione a posteriori del parametro punto di flesso del modello.
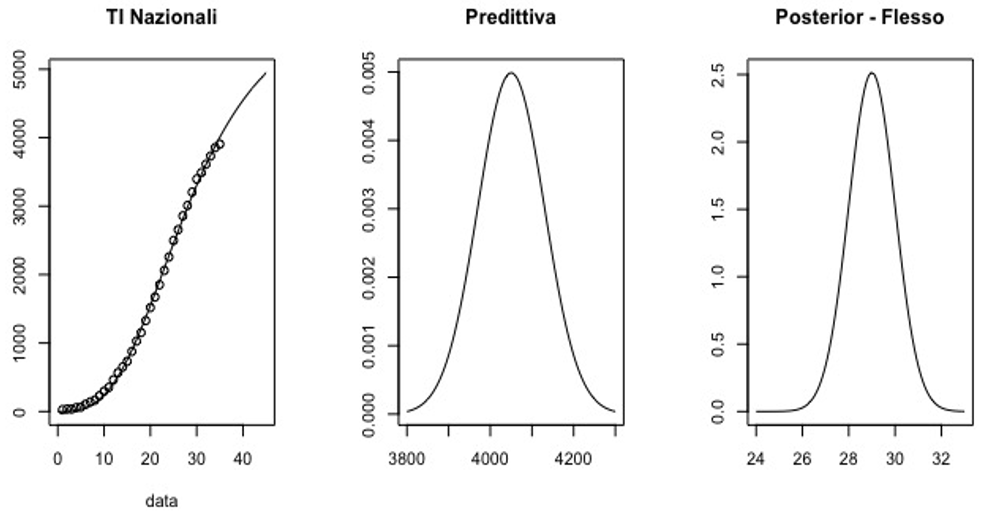
Figura 2: Ricoveri in terapia intensiva (TI)
I grafici rappresentano, nell’ordine modello log-logistico stimato (linea) e i dati osservati (punti); distribuzione predittiva del numero di ricoverati in TI al 30 marzo; distribuzione a posteriori del parametro punto di flesso del modello.
Premesso che la valutazione dell’andamento dell’epidemia su base nazionale comporta di considerare dati rilevati in regioni che presentano molta variabilità comportamentale, si può tuttavia osservare che i modelli stimati hanno un elevato adattamento ai dati. In particolare si verifica che il punto di flesso dei ricoveri in TI sembra raggiunto intorno al 29 giorno dall’inizio della raccolta dei dati (24 febbraio), mentre per il numero dei decessi il flesso è atteso intorno al 41 giorno. La previsione è necessariamente limitata al breve periodo poiché nelle prossime due settimane si dovrebbero avere effetti più rilevanti delle misure restrittive messe in atto e per contro una morbilità superiore in alcuni particolari ambienti (case di riposo, famiglie, comunità in genere).
Per tali eventuali variazioni sistematiche non è sufficiente fare ricorso ai metodi robusti. Mentre possono dare risposte più “spinte” elicitazioni bayesiane. Ma questo richiede una più stretta collaborazione tra statistici e esperti di dominio, oltre che una notevole esperienza sul campo da parte di questi ultimi.
[1] Le analisi complete disaggregate per regione e aggiornate, oltre che di maggior dettaglio si trovano con commenti metodologici e tecnici insieme ai riferimenti bibliografici estesi in https://homes.stat.unipd.it/lauraventura/content/ricerca, pagina dedicata alla ricerca che conduce il gruppo di ricercatori Robbayes-C19 aggregatosi spontaneamente nell’intento di studiare la capacità descrittiva e predittiva a breve termine di modelli statistici robusti, sia in ambito frequentista sia in ambito bayesiano. Obiettivo centrale del gruppo è proporre una procedura di compromesso tra semplicità e accuratezza che sia di facile interpretazione e che possa essere migliorata da contributi rapidamente aggiornabili. Il gruppo è composto da ricercatori dell’Università di Padova (P. Girardi, E. Ruli, L.Ventura), Udine (V. Mameli), Cagliari (M. Musio, W. Racugno), Benevento (L. Greco). Tutti soci della Società Italiana di Statistica.
Riferimenti bibliografici
- Basu, A., Harris, I.R., Hjort, N.L., Jones, M.C. (1998). Robust and efficient estimation by minimising a density power divergence. Biometrika, 85, 549–559.
- Dawid, A.P., Musio, M., Ventura, L. (2016). Minimum scoring rule inference. Scand. J. Statist., 43, 123–138.
- Huber, P.J., Ronchetti, E.M. (2009). Robust Statistics. Wiley, New York.
- Ventura, L., Racugno, W. (2016). Pseudo-likelihoods for Bayesian inference. In: Topics on methodological and applied statistical inference, series studies in theoretical and applied statistics, pp. 205–220. Springer, Berlin.
- Girardi, P., Greco, L., Mameli, V., Musio, M., Racugno, W., Ruli, E., Ventura, L. (2020). Robust inference for nonlinear regression models from the Tsallis score: application to COVID-19 contagion in Italy. (in progress)