StatGroup-19:
Fabio Divino – Università del Molise
Gabriele Fabozzi – Università di Roma “La Sapienza”
Alessio Farcomeni – Università di Roma “Tor Vergata”
Giovanna Jona Lasinio – Università di Roma “La Sapienza”
Gianfranco Lovison – Università di Palermo
Antonello Maruotti – Università di Roma “LUMSA”
Lo studio dell’epidemia di Covid-19 è un tema di ricerca urgente dal quale la comunità statistica non può sottrarsi. In questo lavoro si espongono alcuni approcci metodologici adottati dal gruppo di ricerca StatGroup-19. Vengono ricalcati i metodi adottati ed il percorso logico che ha portato alla scelta di determinati modelli, le insidie dovute alla qualità e definizione dei dati ed infine ad alcune prime stime sul momento di picco dell’epidemia in Lombardia.
Alla fine di febbraio, l’Italia viene improvvisamente investita dall’onda epidemica causata dal contagio del virus SARS-CoV-2. Fin dai primi casi rilevati in Italia, si è avvertita l’esigenza di prevedere l’andamento dell’epidemia di Covid-19 nel nostro paese.
Il susseguirsi di decreti, misure restrittive, e una forte attenzione mediatica e (comprensibile) apprensione da parte della popolazione hanno fatto sorgere in contemporanea molte domande alle quali la statistica e l’epidemiologia possono e devono tentare di dare risposte. Come crescerà il numero di casi positivi? Quando si arriverà ad un picco di contagiati? Il picco sarà sostenuto nel tempo? Come crescerà la domanda di posti letto nei reparti di terapia intensiva?
Rispondere a tali domande consente di alleggerire in qualche misura il già gravoso compito che strutture ed operatori sanitari sono chiamati a svolgere, permettendo di pianificare al meglio le risorse a disposizione. Ci si pone quindi il problema di come utilizzare correttamente e velocemente i dati forniti dalla Protezione Civile nell’ormai consueto bollettino delle 18:00; e fare previsioni su queste cifre per i giorni futuri. Quali indicatori utilizzare? Previsioni di lungo o breve periodo? Quali modelli utilizzare?
Lo scopo di questo articolo è quello di mostrare un primo approccio per la previsione di alcune delle grandezze sopraccitate, in particolare il numero di nuovi casi positivi (e quindi del totale di casi positivi) ed il numero di ricoveri in terapia intensiva dovuti al Covid-19. Si esploreranno brevemente alcune delle questioni riguardanti la natura e la qualità dei dati, ed infine verranno fornite delle prime stime sul momento di picco dell’epidemia.
La natura del dato e del fenomeno: i conteggi
I dati forniti dalla Protezione Civile sono conteggi aggregati riferiti al numero di casi di persone che si ammalano, che guariscono, che muoiono, che vengono ricoverate in terapia intensiva, ecc. Nello specifico queste cifre vengono fornite quotidianamente, e sono suddivise per regione. Ciò che interessa dunque è studiare l’andamento di questi conteggi nel tempo e possibilmente produrre delle previsioni per i giorni successivi.
I conteggi presentano quasi sempre una caratteristica importante: la loro tendenza centrale e la loro dispersione (ovvero media e varianza) cambiano insieme, od in altre parole sono dipendenti. Mentre per dati continui (ad esempio misurazioni d’altezza, peso, temperatura) possiamo avere valori grandi molto vicini, o valori piccoli molto lontani tra loro, tipicamente con i conteggi questo non avviene. Serie di conteggi tendenzialmente grandi sono più variabili di serie di conteggi tendenzialmente piccoli. Questo non è un fatto astratto, ma qualcosa di osservabile e misurabile, ed influenza il modo in cui i conteggi possono essere descritti matematicamente.
La natura del dato sopra descritta è fondamentale per la scelta dei modelli che verranno utilizzati per descrivere il progresso dell’epidemia. Se si considerano modelli parametrici (vale a dire modelli dove si fa un’ipotesi sulla distribuzione del dato che si vuole studiare) è importante che i modelli tengano conto della natura del dato e di eventuali differenze nel comportamento tra media e varianza.
Semplificando, è noto che le epidemie generalmente seguono una prima fase di crescita esponenziale. A questa fase fa seguito un picco (che può eventualmente essere sostenuto per un periodo di tempo) ed infine si ha una decrescita via via che le misure introdotte per contenere la diffusione del virus sortiscono il loro effetto.
Essendo interessati a previsioni nella fase di crescita esponenziale dell’epidemia, si è optato per un modello specifico per conteggi. Tale approccio è più rigoroso dell’alternativa, ossia applicare delle trasformazioni ai conteggi, trattarli come dati continui ed infine utilizzare dei modelli lineari. Quest’ultimi infatti non tengono conto della sopraccitata dipendenza tra media e dispersione, che i dati possono presentare.
È inoltre importante tenere a mente che tali modelli sono appropriati solo per previsioni nel breve periodo (ovvero per descrivere la fase di crescita esponenziale), in quanto non prevedono che l’andamento dell’epidemia possa raggiungere un picco per poi decrescere. Stime riguardanti il picco verranno riportate in seguito, e verranno prodotte con metodi alternativi.
Previsione dei nuovi casi positivi nel breve periodo
L’approccio utilizzato per prevedere il numero di nuovi casi positivi funziona in due passi e tenta di approssimare le due fasi con cui generalmente si individua un “caso”: screening e diagnosi. In questa situazione epidemiologica, il processo di screening ha la seguente forma: gli individui potenzialmente e tendenzialmente positivi si auto selezionano rivolgendosi alle autorità di sanità pubblica oppure vengono individuati in base a connessioni con precedenti casi conclamati. Il processo di diagnosi, invece, avviene per controllo tramite tampone.
Il modello utilizzato quindi si compone delle seguenti fasi: una prima fase in cui si stima il numero di tamponi giornalieri, e successivamente una seconda fase in cui, condizionatamente al numero di tamponi effettuati, si stimano i nuovi casi positivi. In entrambe le fasi le previsioni vengono fatte utilizzando metodologie specifiche per dati di conteggio di cui sopra. In particolare, per la stima del numero dei tamponi si utilizza un modello detto INAR (INteger-valued AutoRegressive Model – Modello autoregressivo a valori interi), mentre per la stima dei nuovi casi identificati viene usata una regressione log-lineare con verosimiglianza Binomiale Negativa [2][3].
Per validare i risultati abbiamo per alcuni giorni stimato il modello su parte dei dati prevedendo gli ultimi tre giorni, sempre con risultati soddisfacenti. Il risultato finale è una previsione del numero di nuovi casi positivi per un orizzonte temporale che abbiamo arbitrariamente fissato a un massimo di tre giorni.

Tabella 1: Previsioni del totale dei casi positivi cumulati basati su dati fino al 9 marzo 2020. Si presentano intervalli di confidenza al 95%.
La Tabella 1 mostra le previsioni per il totale dei casi positivi cumulati fino al 13/03/2020. Tali previsioni si basano sui dati disponibili fino al 09/03/2020, e vengono riportate insieme a degli intervalli di previsione al 95%. Questo approccio ha funzionato bene fino a quando la serie dei casi identificati era allineata temporalmente alla serie del numero di tamponi a cui tali casi si riferivano. Al crescere del livello dei conteggi nei giorni, si è osservato un ritardo tra il primo dato rispetto al secondo difficilmente controllabile: dichiarazioni ufficiali della Protezione Civile lo inquadrano intorno a 4-5 giorni. Si è quindi optato per approcci più flessibili basati sull’uso di tecniche non parametriche (splines) [4] in grado di catturare la maggiore eterogeneità nelle politiche sanitarie di somministrazione dei tamponi, una volta che l’epidemia si è diffusa a più regioni. Tali tecniche non parametriche richiedono tuttavia elevate quantità di dati per dare risultati a bassa incertezza [5] e sono quindi poco affidabili nella prima fase di sviluppo di un’epidemia.
Qualità dei dati: problemi con le definizioni
Nel processo di analisi del numero dei “nuovi casi attualmente positivi” (e quindi dei totali) ci si è presto imbattuti in un problema non da poco, vale a dire il modo in cui tale variabile viene calcolata. Tale dato può infatti trarre in inganno se lo scopo è quello di studiare l’andamento dell’epidemia oltre le fasi iniziali, in quanto diversa dal “numero di nuovi contagiati”. Se si prende come riferimento temporale un periodo di 24 ore, il numero di “nuovi casi attualmente positivi” (abbreviato Ca) è infatti una combinazione di tre componenti: il numero di nuovi contagiati (Ct), il numero di nuovi guariti (Cg) ed il numero di nuovi decessi (Cd) in quell’arco di 24 ore. Più precisamente, si avrà che
Ca = Ct – Cg – Cd
In altre parole, il numero di “nuovi casi attualmente positivi” mostra il numero di nuovi contagiati al netto dei guariti e dei deceduti nelle ultime 24 ore. Tale numero può eventualmente essere negativo, in quanto è possibile che i nuovi guariti o i nuovi decessi (o la loro somma) superino il numero dei nuovi contagiati in un determinato giorno. Confondere tale variabile con il numero di nuovi contagiati è un errore che ha spesso tratto in inganno i media d’informazione, generando sovente confusione nell’opinione pubblica.
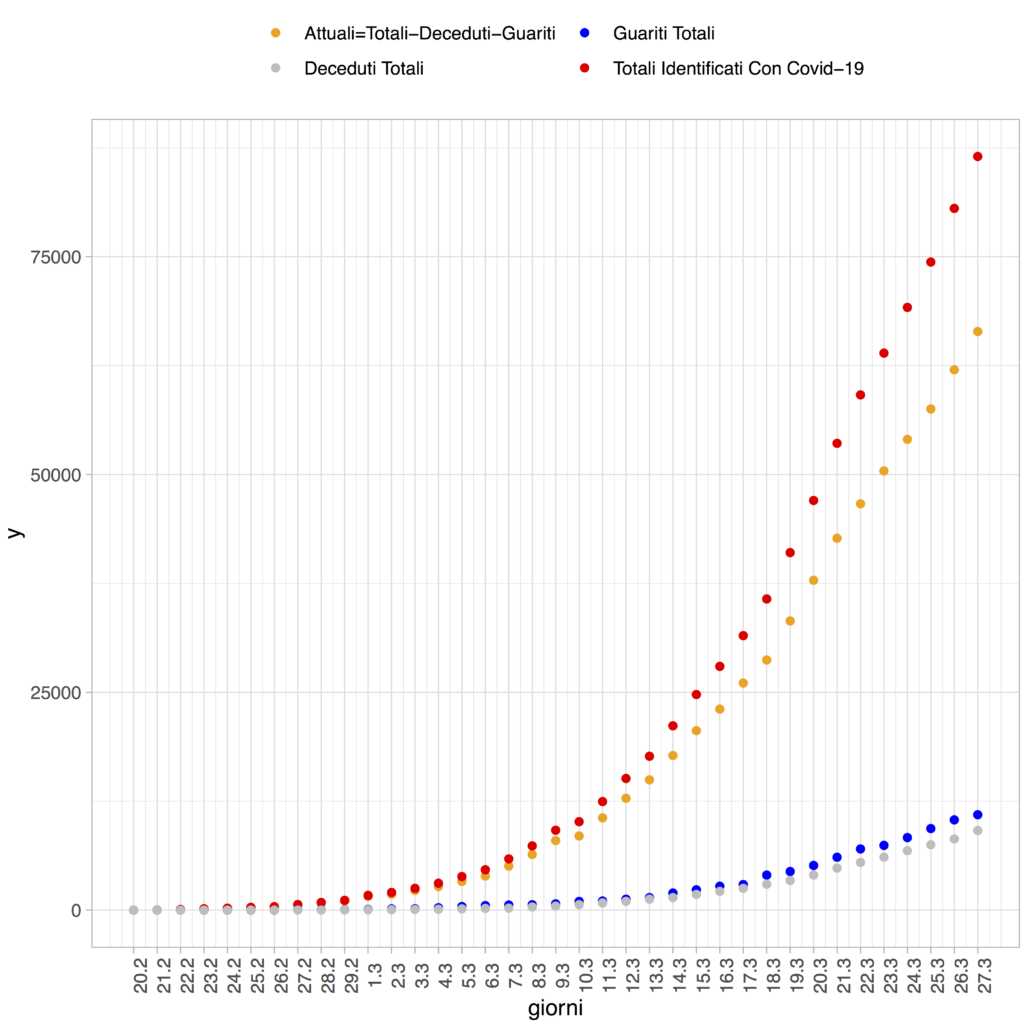
FIgura 1: Conteggi riportati dalla Protezione Civile e utilizzati nella definizione dei casi “attualmente positivi” (dati al 27 Marzo 2020). I conteggi sono a livello nazionale.
Altra questione non poco rilevante è il fatto che tra i nuovi casi attualmente positivi vi è una forte prevalenza di casi con gravi sintomatologie e per i quali il tampone è stato effettuato da 1 a 10 giorni prima. Ciò può portare a previsioni eccessivamente pessimistiche del progresso dell’epidemia, o comunque solo parzialmente rappresentative della reale situazione.
In base a tali considerazioni, abbiamo sottolineato come il numero di nuovi casi attualmente positivi non fosse un buon indicatore per lo studio a breve termine del progresso dell’epidemia, ed essendo i casi totali affetti da elevata eterogeneità si è iniziato a lavorare su altre grandezze. Sempre con l’obiettivo di fornire previsioni per facilitare la programmazione delle risorse sanitarie in questa fase di crescita dell’epidemia, si è volto lo sguardo verso un altro conteggio a tal fine rilevante: il numero dei pazienti ricoverati in terapia intensiva.
Previsione del totale dei ricoveri in terapia intensiva
Un approccio diverso rispetto a quello utilizzato per prevedere il numero di totale di nuovi casi positivi viene quindi definito ed applicato al totale dei ricoveri in terapia intensiva per ogni regione (per un’illustrazione non tecnica sulle previsioni dei ricoveri in terapia intensiva si veda [1]). Un esempio è riportato nella Tabella 2 in cui vengono confrontate le previsioni con i valori osservati e la capienza regionale.
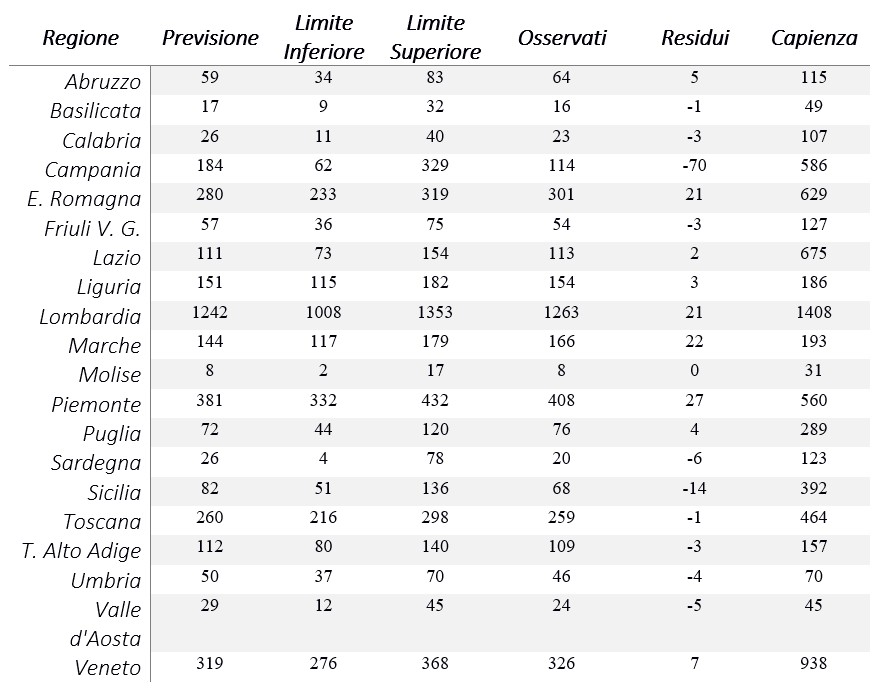
Tabella 2: Esempio di previsioni per i ricoveri in terapia intensiva al 26 marzo 2020. Gli intervalli di confidenza riportati sono al 99%.
Previsioni nel medio periodo: il picco dei ricoveri
Le previsioni dei nuovi ricoveri in terapia intensiva possono anche fornire dei primi indizi sul momento in cui l’epidemia è entrata in una fase di picco. Questi sono definiti semplicemente come la differenza fra il numero di ricoverati in terapia intensiva in un determinato giorno rispetto al giorno precedente. Le stime sul momento di picco vanno tuttavia contestualizzate su base regionale, in quanto non solo il virus ha preso piede in alcune regioni prima di altre, ma le misure di contenimento non sono state applicate contemporaneamente su tutto il territorio nazionale. Nella Figura 2 sono riportate le curve dei casi cumulati distinti per area geografica. La Lombardia è stata riportata da sola poiché rappresenta da sola la maggioranza dei casi a livello nazionale. È molto evidente dal grafico la diversa situazione nelle varie aree del paese. Al Centro e nel Mezzogiorno l’epidemia parte già con le misure di contenimento in atto: questo ne riduce la velocità di crescita rispetto alle regioni del Nord e, sperabilmente, anche la dimensione finale.
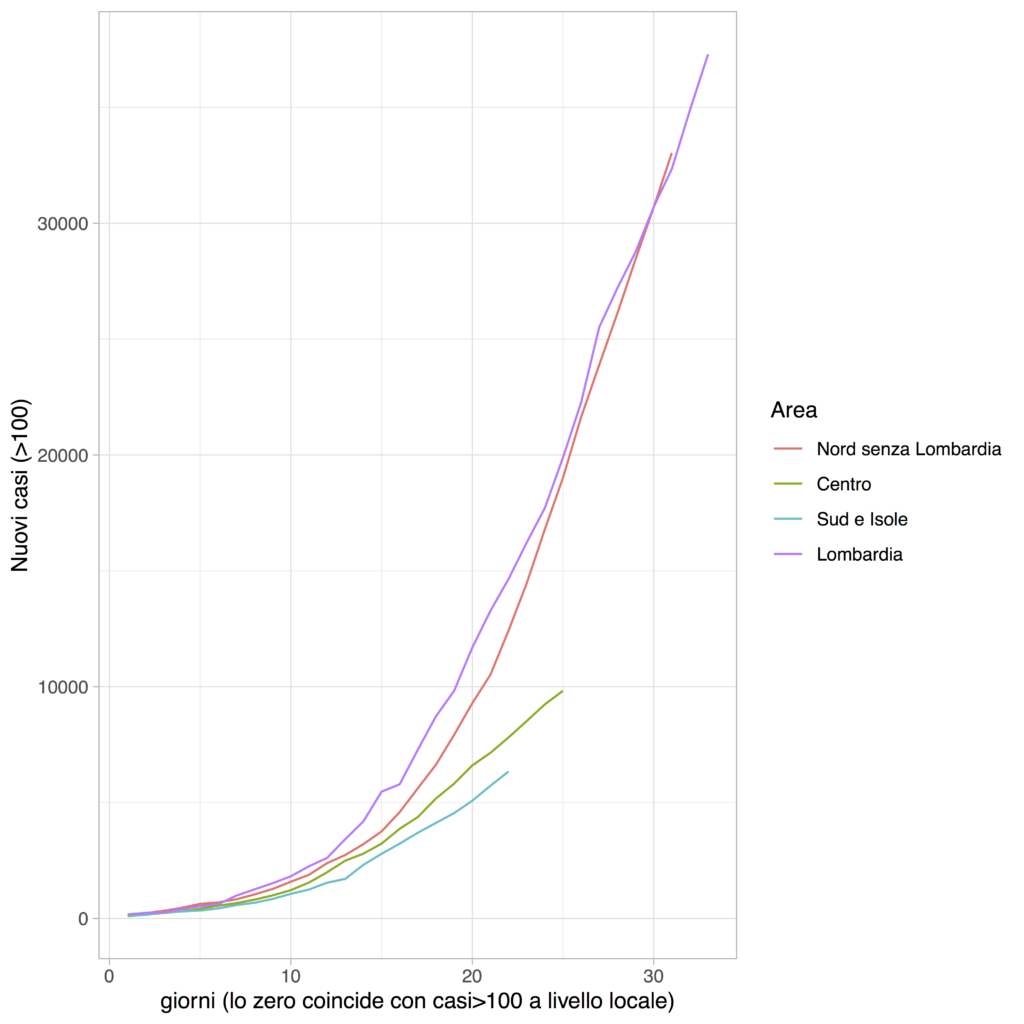
Figura 2: Numero di casi positivi distinti per area geografica, le curve iniziano quando il numero di casi positivi supera le 100 unità nell’area.
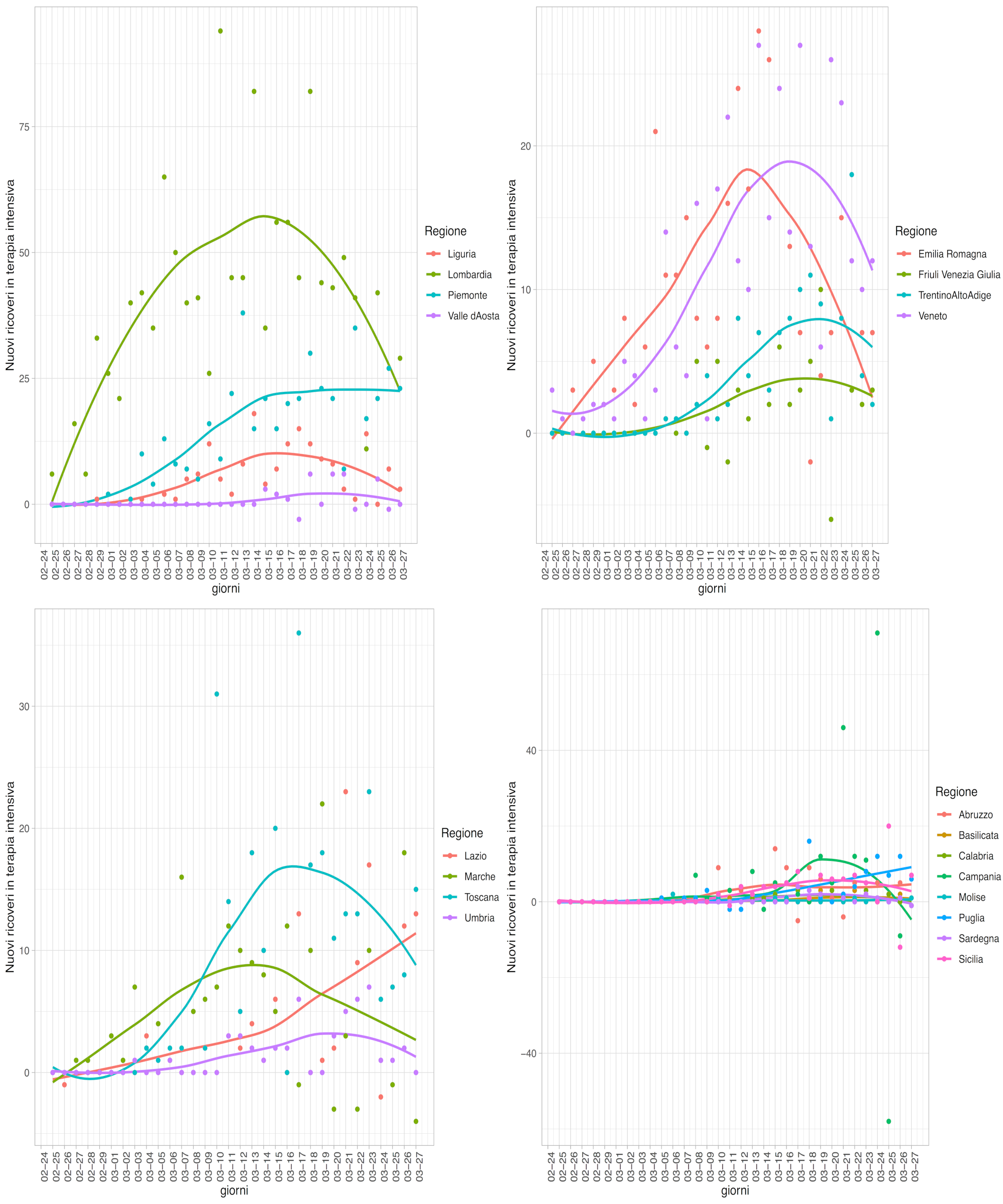
In Figura 3 si mostrano i numeri di nuovi ricoveri in terapia intensiva ogni giorno dal 24/02 al 27/03, disaggregati per regione. Le curve sovrapposte mostrano delle stime delle tendenze di fondo. Prendendo come riferimento la Lombardia, tale tendenza di fondo sembra mostrare che l’entrata nella fase di picco per i nuovi ricoveri sia avvenuta nel periodo 21/03-26/03. Se si ipotizza un ritardo di 7-10 giorni tra il picco dei ricoveri in terapia intensiva ed il picco dei casi positivi, una prima stima dell’entrata nella fase di picco per il numero di casi positivi in Lombardia può essere individuata intorno al 18/03. Si noti la differenza di scala tra le diverse regioni.
Per le altre regioni ed a livello nazionale, le stime del momento di entrata nella fase di picco sono tutte superiori al periodo 22/03-25/03. Tali stime vanno quindi prese con riserva per via dell’impossibilità di quantificare, al momento in cui venivano fatte le stime, gli effetti delle misure restrittive che nel frattempo erano sopraggiunte. Le tendenze di fondo nella figura suggeriscono tuttavia come il numero di nuovi ricoveri segua un andamento cosiddetto logistico, seppur in modo diverso tra regioni.
Il numero di ricoverati in terapia intensiva permette quindi di avere una fotografia più complessiva dell’andamento dell’epidemia, non limitata alla fase di crescita esponenziale della stessa. Utilizzando dei modelli di tipo logistico, più precisamente GLM (Generalized Linear Models – Modelli lineari generalizzati) con funzione risposta logistica generalizzata e distribuzione Binomiale Negativa [1], è stato possibile dunque avere delle prime stime attendibili, limitatamente ad alcune regioni, dell’andamento dell’epidemia.
Non diversamente da altri casi, è importante contestualizzare i risultati e avere ben presenti i limiti che tali approcci e modelli comportano. In primo luogo, è importante sottolineare le forti differenze negli andamenti tra le diverse regioni, già sottolineate in precedenza. In secondo luogo, è bene tenere a mente che l’efficacia di tali modelli è tanto limitata almeno quanto la capacità di quantificare fenomeni che possono inficiarne la validità, tra i quali ad esempio il trasferimento improvviso da una regione ad un’altra di pazienti in terapia intensiva, o l’adozione di comportamenti a rischio quali il rientro di molti dalle regioni del Nord al Sud. Infine, la spesso scarsa qualità dei dati forniti all’Istituto Superiore di Sanità (ISS), frutto della combinazione tra la necessità di fornire dati in tempo reale a causa dell’emergenza e l’eterogeneità nei modi di gestione e trasmissione dei dati a livello locale, è un fattore che può essere dannoso ai fini dell’attendibilità delle previsioni.
Emerge quindi da tali esperienze come, oltre alla specificazione di una modellistica adatta al fenomeno di studio, sia compito dello statistico avere un’immagine chiara della natura e dei problemi dei dati a disposizione. Inoltre, si è visto come studiare un fenomeno in corso necessiti di una capacità di adattamento in itinere in base alla piega che il fenomeno stesso sta prendendo o sulla base di nuove informazioni sulla natura dei dati, come nel caso della previsione dei casi positivi.
[1] Technical note on Short-term predictions of daily intensive care unit (ICU) hospitalizations due to Covid-19. StatGroup-19. https://statgroup-19.blogspot.com/p/short-term-predictions-of-daily.html
[2] Maria Eduarda Silva. “Modelling Time Series of Counts: an Inar Approach.” Textos de Matematica, DMUC, 47, 107-122. (2015).
[3] James G. Booth, George Casella, Herwig Friedl, James P. Hobert. “Negative Binomial Loglinear Mixed Models”. Statistical Modelling. 3. (2002).
[4]Trevor J. Hastie, Robert J. Tibshirani. Generalized Additive Models. Chapman and Hall. (1990). ISBN 978-0-412-34390-2.
[5] Simon N. Wood Generalized Additive Models: An Introduction with R (2nd ed). Chapman & Hall/CRC. (2017). ISBN 978-1-58488-474-3