Federico Brogi – ISTAT [1] [2]
Barbara Guardabascio – ISTAT [1] [3]
Mediante un modello molto parsimonioso si stima l’evoluzione del tasso di diffusione del COVID-19, l’effetto, in tempo reale, di ogni misura governativa sulla diffusione del virus e la possibile data di uscita. Elaborato a due settimane dall’inizio dell’epidemia in Italia, e aggiornato in questi giorni (5 aprile NdR), il modello conferma la sua solidità nel prevedere l’andamento del tasso di diffusione. Si rivela, inoltre, un valido framework teorico, altamente replicabile sostituendo i dati sui casi in Italia con quelli di diversi paesi, e in grado di offrire indicazioni chiare in termini di elaborazione delle politiche.
L’epidemia da COVID-19 iniziata in Cina nel dicembre del 2019 è arrivata a colpire tutto il mondo raggiungendo livelli pandemici. La sua rapida diffusione ha costretto i governi ad emanare forti misure restrittive
Il modello
In base al loro studio di Chenlin et al.(2020), è possibile suddividere la popolazione infetta in tre sotto-gruppi:
- Ic : R+ → ℤ individui contagiati, rilevati dal tampone
- Ia : R+ → ℤ individui contagiati attivi, non rilevati dal tampone
- Iq : R+ → ℤ individui contagiati non confermati, in quarantena
Il numero totale delle infezioni è dato dalla equazione:
I(t) = Ic(t) + Ia(t) + Iq(t) (1)
Il processo di diffusione del virus parte dal paziente zero il cui tasso di contagio, prima che gli venga confermata la quarantena, risulta essere pari a β.
A tale parametro si collega il numero riproduttivo R0, è possibile distinguere tre diversi fasi dell’epidemia:
- Supercritica: R0 > 1, in questo caso l’epidemia presenta una crescita esponenziale
- Critica: R0 = 1, l’epidemia permane per un lungo periodo
- Sub-critica: R0 < 1, l’epidemia risulta controllata.
Noto che R0 converge asintoticamente al seguente valore: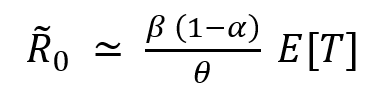
dove α ∈ [0,1] rappresenta la probabilità di quarantena, θ ∈ [0,1] la precisione dei tamponi e E[T] = 7.5, al fine di contenere il valore di R0 è possibile attuare diverse strategie:
- Ridurre il tasso di contagio β evitando il contatto negli spazi pubblici tra gli individui.
- Rendere il valore θ dei controlli prossimo ad 1, migliorando la precisione delle diagnostiche ed incrementando il numero di test (trasformando Ia in Ic).
- Incrementare il tasso α di quarantena al fine di isolare i casi confermati ed evitare il contagio (trasformando Ia in Iq).
I valori di α proposti da Chenlin et al. crescono, all’aumentare della capacità restrittiva delle policy messe in atto, da Misure deboli = 0.2 a Misure molto forti = 0.8. Nella tabella che segue si ripropone una calibrazione del parametro α rispetto alle principali policy adottate dal governo italiano e alla percentuale di popolazione coinvolta nel provvedimento.
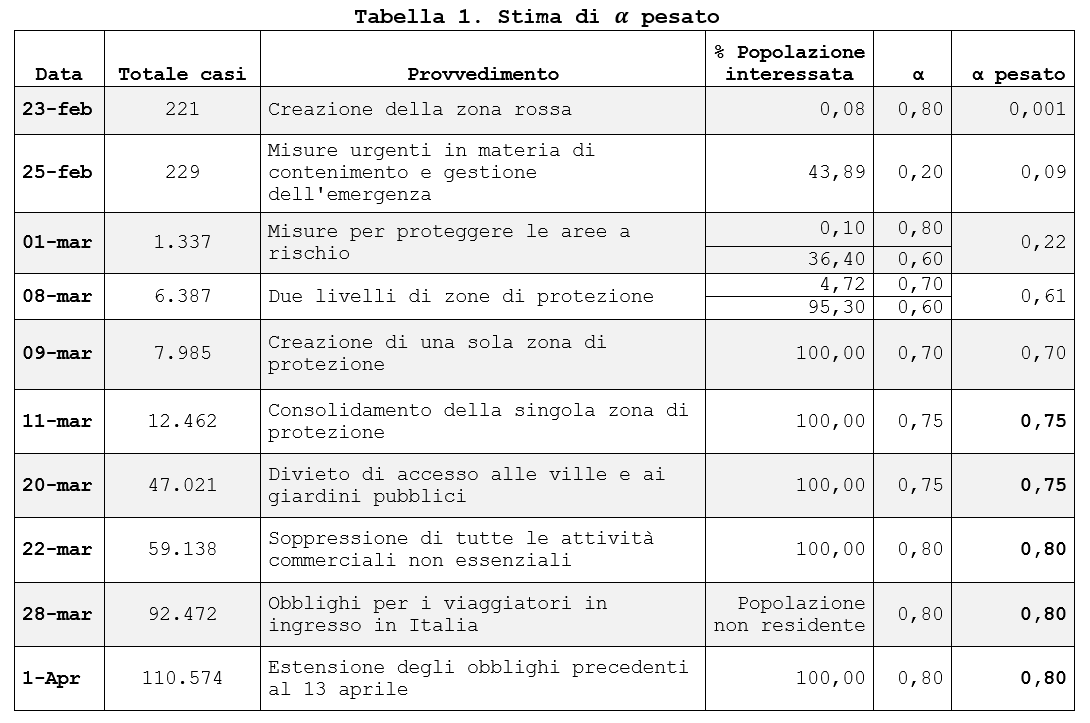
Si noti che i provvedimenti del 20 Marzo e del 28 Marzo non comportano variazioni del parametro α in quanto il primo influisce direttamente sulla stima di β (Ord. Min. Salute 20-Marzo), il secondo rivolto a popolazione non residente (Ord. Min. Salute 28-Marzo). Il provvedimento del 1 Aprile estende le restrizioni al prossimo 13 aprile.
L’effetto delle policy
Per l’esercizio empirico sono stati adottati dati giornalieri della Protezione Civile relativi al periodo 21/02/2020–6/4/2020 per le variabili: nuovi attualmente positivi, totale casi e tamponi giornalieri. La disponibilità di altre variabili apre la possibilità in futuro ad alimentare il modello con ulteriori elementi e/o l’eventualità di effettuare stime su altri aggregati.
Individuate le variazioni indotte sui singoli parametri dalle diverse policy adottate dal governo Italiano è stato possibile procedere alla ricostruzione di una nuova curva teorica vincolata, a partire dalla quale, si è stimato l’effetto (in termini percentuali) di contenimento del contagio generato da ciascuna policy riassunto nella seguente tabella.
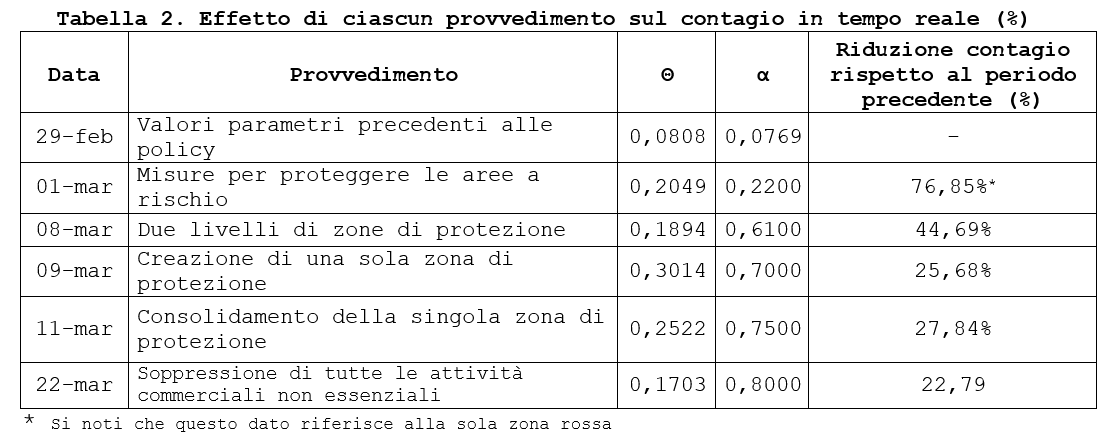
Considerando l’effetto cumulato delle policy attuate dal governo, il modello stima un guadagno del 91.5% rispetto alla curva teorica del contagio, utilizzata come riferimento.
Le simulazioni nella tabella seguente forniscono una stima del guadagno che si ottiene al variare del tipo di policy adottato, sempre nel confronto con la curva teorica e al caso Italia.
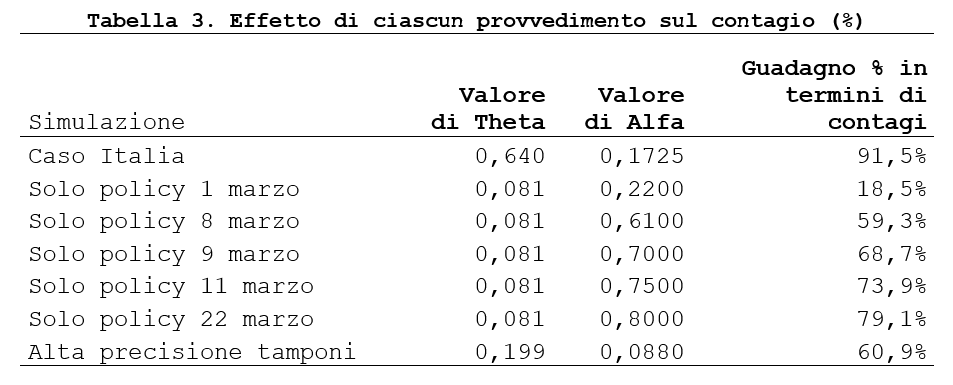
All’aumentare del livello di quarantena il guadagno rispetto alla curva teorica cresce fino al 79,1%. Viceversa il guadagno che si otterrebbe aumentando la precisione dei tamponi, al netto di policy di quarantena si attesta intorno al 60,9%, sottolineando quanto la capacità diagnostica sia un fattore contentivo del contagio esattamente quanto le politiche di tipo restrittivo.
Previsione dei contagi in Italia
Nell’analisi sono stati considerati tre possibili scenari utilizzando come benchmark un andamento del virus in Italia identico a quello della Cina, un secondo intermedio che ipotizza il caso italiano e l’ultimo che individua la frontiera massima che si potrebbe raggiungere in termini di contagi.
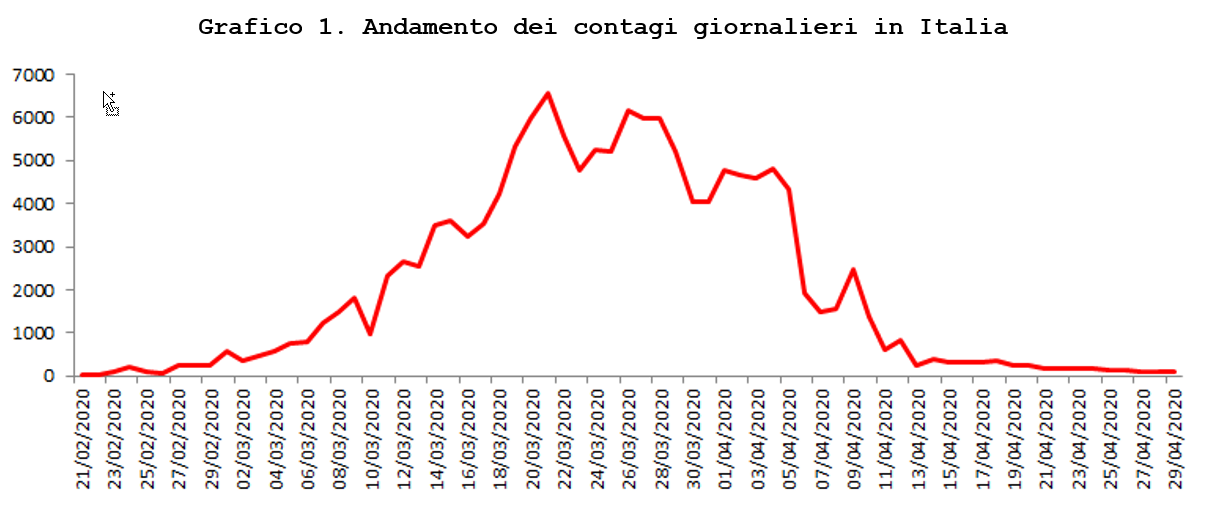
Nell’ipotesi intermedia, che si ritiene più vicina al caso italiano si è stimato il superamento del picco dei contagi giornalieri dopo il 20 marzo, per poi arrivare ad un numero di contagi prossimi a zero intorno al 29 aprile. Nel grafico che segue si ripropone un aggiornamento della previsione per le prossime 3 settimane.
[1] Il testo e il contenuto di questo articolo sono espressione della visione degli autori e non dell’istituto per il quale lavorano
[2] fedebrogi@istat.it
[3] guardabascio@istat.it
Riferimenti bibliografici
- Chenlin G., Wei J., Tianyuan Z. and Ban Z. (2020), Mathematical recommendations to fight against COVID-19
- Shao N., Cheng J. and Chen W. (2020), The reproductive number of COVID-19 based on estimate of a statistical time delay dynamic system, medRxiv, Cold Spring Harbor Laboratory Press
- Protezione Civile (2020). Chronology of main steps and legal acts taken by the Italian Government for the containment of the COVID-19 epidemiological emergency. Updated at 12 of March 2020
