Bruno Chiandotto – Università di Firenze
In questa pandemia gli organi di governo devono ricorrere a strumenti avanzati di inferenza statistica causale quali i modelli ad equazioni strutturali. Tali modelli consentono di valutare l’effetto, diretto e indiretto (e le loro interazioni), di altri fattori causali che possono incidere in modo anche molto rilevante sull’evoluzione del fenomeno. L’impiego di modelli ad equazioni strutturali, inquadrato in una prospettiva decisionale di analisi statistica dei dati, consente una valutazione simultanea dell’impatto sanitario, di quello economico e di quello socio-psicologico, di tutti i fattori causali.
Le istituzioni sanitarie e di governo nazionale e locale, le organizzazioni sindacali e di categoria, le famiglie e i singoli cittadini chiedono alla comunità scientifica di fornire, riguardo l’evoluzione fenomeno epidemico COVID-19, risposte ai seguenti interrogativi:
- Quanti individui risulteranno contagiati?
- Quanti contagiati non riusciranno a sopravvivere (morti)?
- Quale è la presumibile data di manifestazione più intensa (picco) dell’epidemia?
- Quale è la presumibile data di esaurimento del processo epidemico?
- Quale è l’effetto dei provvedimenti di potenziamento delle strutture sanitarie e delle misure restrittive posti in essere dagli organi di governo nazionale e locale?
- Le misure adottate riescono a rallentare i tassi di diffusione del contagio?
- Le misure adottate riescono a ridurre il numero complessivo di contagiati e di morti?
L’evoluzione tipica dei fenomeni epidemici si caratterizza per una fase iniziale di sviluppo moderato cui segue una fase di accelerazione che si attenua con il passare del tempo con tassi di incremento che si riducono progressivamente fino ad annullarsi quando l’intera popolazione interessata risulta contagiata (livello di saturazione del fenomeno).
Una possibile prima risposta che gli statistici possono dare ai sette quesiti elencati può essere basata sulla stima di un modello previsionale di tipo logistico [1].
Il modello logistico, dalla sua iniziale formulazione (Verhulst, 1838), è stato impiegato con successo, in vari contesti operativi, per rappresentare l’evoluzione dei fenomeni di tipo epidemico per il suo elevatissimo grado di approssimazione alla realtà.
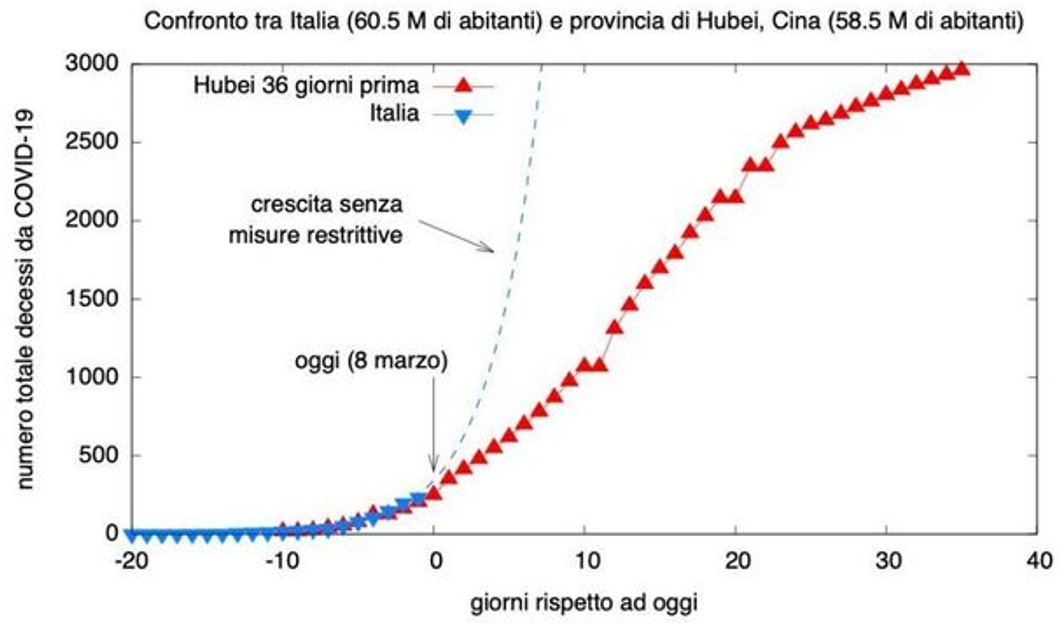
Il grafico sotto riportato, ripreso dal recente articolo “L’epidemia rallenterà certo prima di Pasqua ma non è una buona notizia” scritto da Giorgio Parisi e Luca Foresti, evidenzia in modo molto chiaro l’andamento logistico del COVID-19.
Anche se il modello esponenziale e il modello logistico rappresentano adeguatamente la fase iniziale di sviluppo dei fenomeni epidemici, la “bontà” rappresentativa di un modello previsionale deve essere sempre valutata tenendo conto dell’intero “ciclo di vita” del fenomeno analizzato, dal suo manifestarsi al suo esaurimento.
Pertanto, l’attribuzione di una valenza causale alle misure restrittive poste in essere quali determinanti della variazione dell’andamento del fenomeno nella provincia di Hubei, basata sul modello esponenziale, è del tutto priva di fondamento, l’unica corretta conclusione cui si può pervenire nel caso in esame è che il modello esponenziale non è in grado di rappresentare adeguatamente il fenomeno analizzato.
Volendo pervenire a delle conclusioni in merito ad interventi che si ritiene possano incidere sull’evoluzione naturale di un fenomeno epidemico, limitandosi alla osservazione di figure, il confronto non deve essere fatto tra il dato teorico derivante da un modello e il dato empirico osservato ma tra valori teorici derivanti dalla stima del modello utilizzando i dati osservati prima dell’applicazione degli interventi, e quelli derivanti dalla stima dello stesso modello sui dati osservati dopo un ragionevole lasso di tempo trascorso dall’attivazione degli interventi.
La stima di un modello logistico, utilizzando i dati disponibili a livelli territoriali di riferimento significativi (nazionale, regionale, provinciale, comunale, …), fornisce, in via di prima approssimazione, una misura teorica del numero cumulato di soggetti contagiati, del numero cumulato di decessi, del numero giornaliero di contagiati e di decessi nell’arco temporale di osservazione e in tempi successivi (previsione). La previsione di tali indicatori, può costituire un utile base conoscitiva di riferimento per l’adozione di efficaci politiche di intervento.
Inoltre, se si confrontano i valori teorici (valori interpolati) forniti dal modello in due momenti (giorni) diversi adeguatamente distanziati, si perviene, in via di prima approssimazione, anche, come segnalato, attraverso il semplice confronto visivo, ad una valutazione dell’impatto degli interventi decisi dalle autorità di governo nazionale e locale.
L’impiego del modello logistico fornisce, però, soltanto una risposta parziale alle domande che gli stakeholders possono formulare e rappresenta solo il primo passo dell’analisi che gli statistici possono svolgere per soddisfare esigenze conoscitive immediate finalizzate all’attivazione di interventi urgenti quali, ad esempio, l’adeguamento, in termini di personale, di strutture e di strumenti tecnici, del sistema sanitario.
Per soddisfare le esigenze conoscitive degli organi di governo in modo veramente efficace è necessario ricorrere all’impiego di strumenti metodologici più avanzati di inferenza statistica causale quali i modelli ad equazioni strutturali. Tali modelli consentono di valutare l’effetto, diretto e indiretto (e le loro interazioni), di altri fattori causali (oltre altre agli interventi degli organi di governo) che possono incidere in modo anche molto rilevante sull’evoluzione del fenomeno epidemico quali l’età, il genere, la condizione occupazionale, l’attività lavorativa svolta, i fattori di contesto territoriale (opportunamente declinati), gli stili di vita e di comportamento individuale, ecc. .
L’impiego di modelli ad equazioni strutturali inquadrato in una prospettiva decisionale di analisi statistica dei dati, consente, inoltre, una valutazione simultanea soddisfacente dell’impatto sanitario, di quello economico e di quello socio-psicologico, di tutti i fattori causali, sopra richiamati.
Un’avvertenza finale: la base conoscitiva che gli statistici sono in grado di fornire risente di tutti limiti propri dell’uso di modelli ed è strettamente condizionata dalla qualità dei dati utilizzati.
[1] Considerando la formulazione del modello logistico
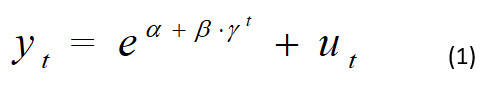
dove, t =1, 2, …..T rappresenta il tempo di osservazione delle manifestazioni del fenomeno, ad esempio giorno e T il numero di osservazioni disponibili) yt , l’intensità del fenomeno (numero cumulato di persone infette o di decessi), α, β e γ , i parametri che specificano il modello e che devono essere stimati utilizzando i dati disponibili, la componente accidentale.
Il modello stimato
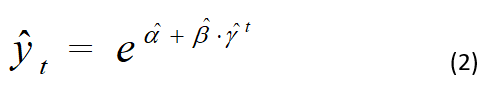
ad un livello territoriale di riferimento significativo, fornisce una misura teorica dell’intensità del fenomeno indagato (numero cumulato di contagiati o di decessi).
Attribuendo a t i valori T+1, T+2, … , T+h ( h → ∞ ) si ottiene la previsione dei dati di interesse.
Il modello (2) non fornisce soltanto i valori teorici ma consente anche, attraverso il calcolo della derivata rispetto a t, di ottenere la stima dell’intensità giornaliera del fenomeno oggetto di analisi, il massimo della derivata fornisce la stima del ‘picco’.
Riferimenti bibliografici
- Chiandototto, Corona virus e statistica, Nota didattica, Corso di Dottorato in Statistica dell’Università degli Studi di Firenze, 2020.
- Bacci e B. Chiandotto. Introduction to Statistical Decision Theory, Utility Theory and Causal Analysis, Chapman and Hall/CRC, 2019.