Michela Baccini – Università di Firenze
Giulia Cereda – Università di Firenze
Cecilia Viscardi – Università di Firenze
Fabrizia Mealli – Università di Firenze
Il nuovo coronavirus (il cui nome scientifico è SARS-CoV-2) è un virus che si contraddistingue per la forte contagiosità. La malattia COVID19 ad esso associata può comportare la necessità di ricovero in terapia intensiva e, nei casi più gravi, può condurre alla morte. In assenza di una cura efficace e/o di un vaccino, l’unica possibilità di arginare la diffusione dell’epidemia risiede nel distanziamento sociale (Lin et al., 2010). Seguendo l’esempio della Cina, l’Italia ha quindi attuato un graduale “lockdown”, iniziando da piccole aree per poi estendere le misure di contenimento a tutta la nazione. In queste brevi note proponiamo un metodo, basato su un modello SIRD calibrato sul numero di decessi giornaliero, che può essere impiegato per monitorare gli effetti e valutare l’impatto a breve e medio termine delle politiche di contenimento sull’evoluzione dell’epidemia e sul sistema sanitario. Il modello è qui applicato ai dati della regione Toscana.
Monitorare e prevedere l’evoluzione dell’epidemia: il modello SIRD
Sotto alcune assunzioni la complessa dinamica di diffusione di un’epidemia può essere descritta da modelli che consentono di prevedere la futura evoluzione del contagio. Il modello qui adottato, rappresentato in Figura 1, è di tipo SIRD (Amenaghawon, Aboubakary, 2015): esso suddivide la popolazione ad ogni istante temporale nelle seguenti 4 categorie o compartimenti: suscettibili S(t), infetti I(t), guariti R(t) e morti D(t).
La numerosità di ogni gruppo varia nel corso del tempo e la dinamica di diffusione dell’infezione è regolata dai tassi β, α, δ, descritti in Tabella 1. Nella trasmissione del virus, gioca un ruolo fondamentale il parametro R0 (ricavabile dai tassi di transizione tra compartimenti) che, se la popolazione è numerosa, può essere interpretato come il numero di nuovi infetti che si sostituiscono ad un individuo che guarisce o muore. Questa definizione consente di comprendere che la diffusione di un’epidemia può arrestarsi solo se R0 < 1 , ovvero quando il numero di individui che escono dal compartimento degli infetti è maggiore di quelli che vi entrano. Le assunzioni del modello SIRD da noi utilizzato sono descritte in Tabella 2.
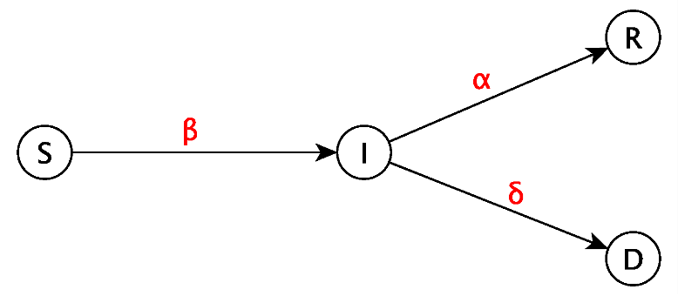
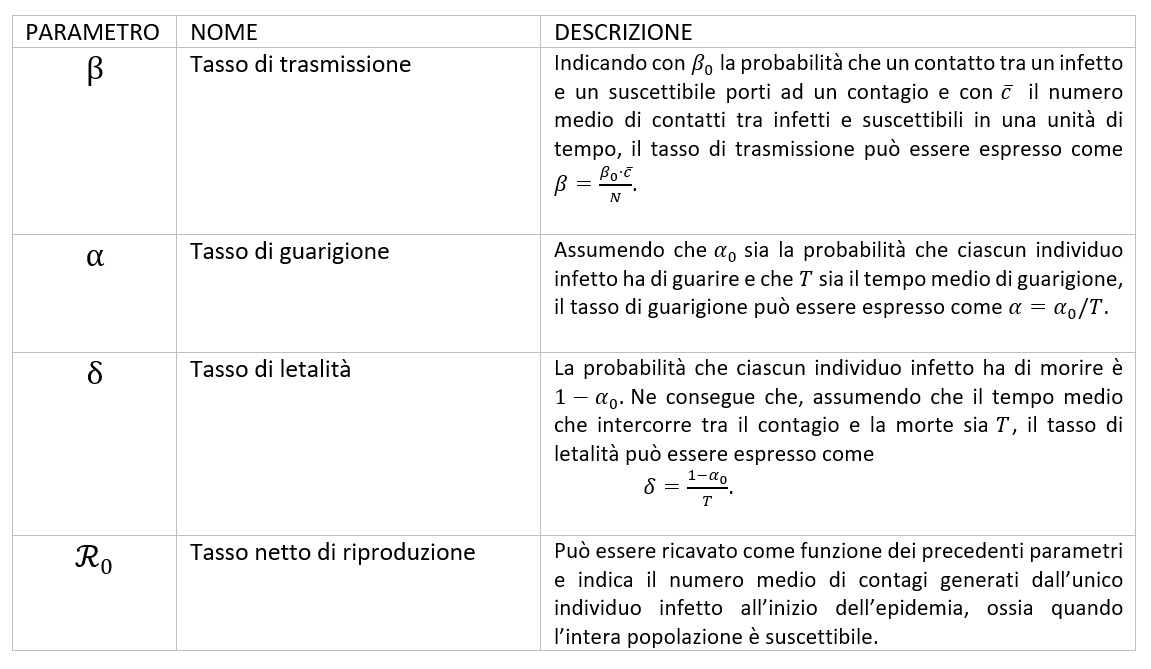
Tabella 1: Descrizione dei parametri del modello SIRD.

Tabella 2: Assunzioni del modello SIRD.
Calibrazione del modello
La Protezione Civile mette a disposizione diversi dati giornalieri, tra cui il numero di positivi, che dipende tuttavia dal numero di tamponi effettuati e può quindi discostarsi notevolmente dal numero effettivo di infetti. Ad esclusione delle fasi iniziali dell’epidemia, si può presupporre invece che tutte le morti di persone affette da COVID-19 siano rilevate. Per questo calibriamo i parametri del nostro modello solo con il numero di decessi giornaliero; i risultati che seguono sono del tutto preliminari e si riferiscono alla regione Toscana.
In che direzione stiamo andando? Un’ipotesi ottimistica di evoluzione dell’epidemia
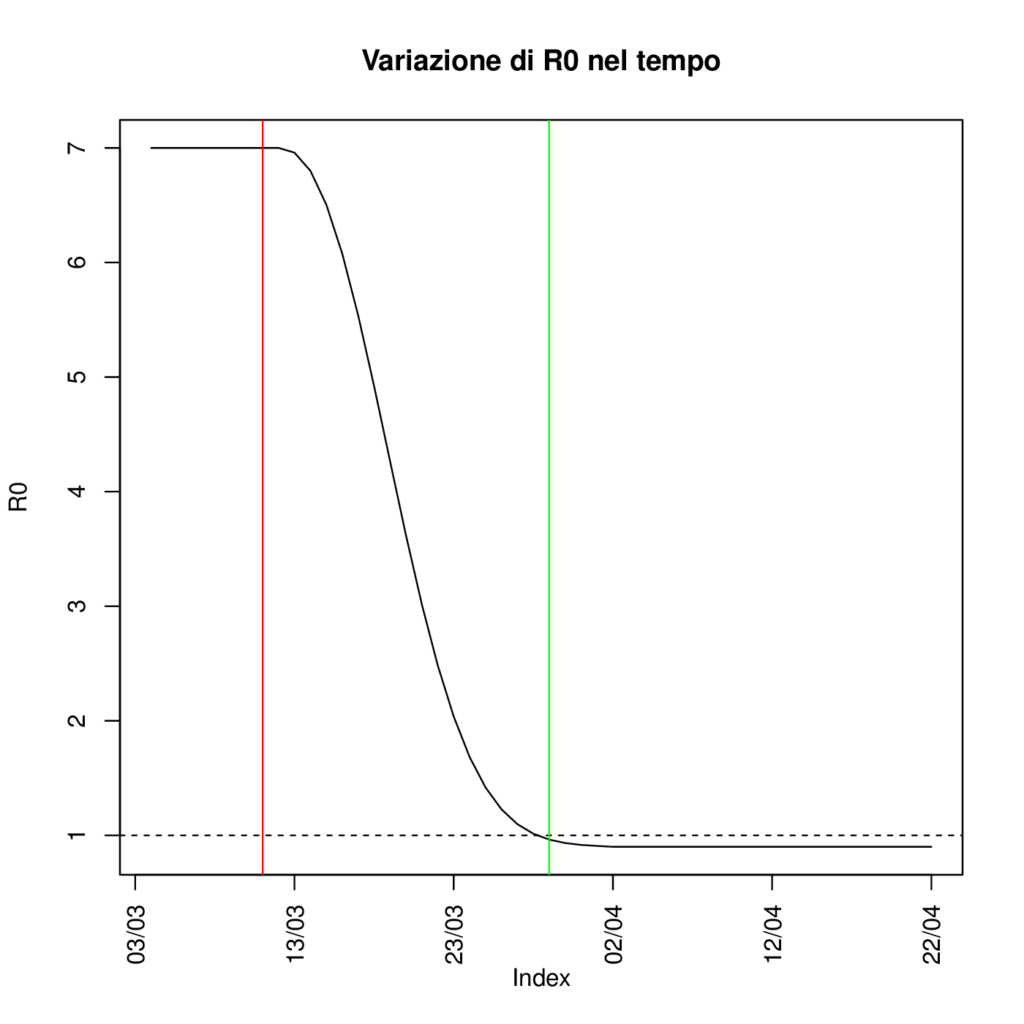
Figura 2
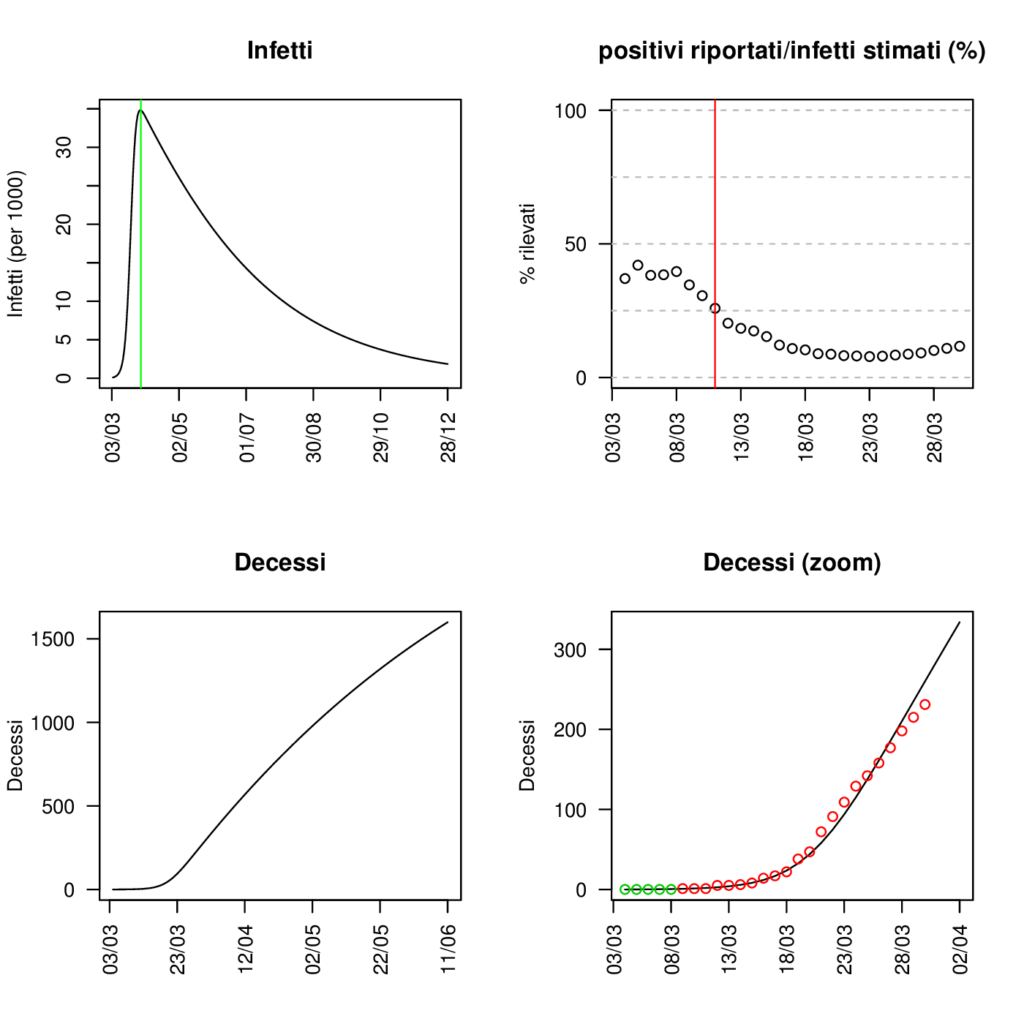
Figura 3
In Figura 3 presentiamo le previsioni del nostro modello SIRD sul numero di infetti, di decessi, e sul rapporto percentuale tra tamponi risultati positivi e numero di infetti stimato per la regione Toscana, ottenute utilizzando valori dei parametri corrispondenti a un R0 variabile nel tempo rappresentato in Figura 2. In particolare, partendo da un valore di R0 stimato per il periodo pre-contenimento intorno a 7, assumiamo che l’ R0 decresca a partire dal giorno successivo al decreto Conte del 10 marzo per arrivare al di sotto della soglia di 1 entro la fine del mese. E’ importante sottolineare come queste previsioni si basino su uno scenario semplificato di successo del lockdown che al momento si mostra coerente con l’evoluzione dei decessi osservata, ma che dovrà essere confermato alla luce dei dati di mortalità dei prossimi giorni; pertanto devono essere considerate con molta cautela. Sotto questa ipotesi di progressivo declino dell’ R0, il picco dell’epidemia si raggiungerebbe a una quota di circa 35’000 infetti, a fine marzo. Nonostante, in accordo alla nostra ipotesi, a tale data sia già inferiore a 1, si osserva che successivamente la curva decresce in modo lento. Questo suggerisce che un’eventuale interruzione precoce delle misure restrittive, attuata prima che il numero di infetti sia sensibilmente diminuito, potrebbe portare ad una nuova escalation di contagi, vanificando i sacrifici dei mesi precedenti. Di fatto non basta “soltanto” raggiungere un R0 < 1 ma serve mantenerlo abbastanza a lungo per fare esaurire o ridurre drasticamente il numero di contagi. Per quanto riguarda la percentuale dei positivi confermati sul totale degli infetti ottenuti da modello, stimiamo che attualmente si stia rilevando solo il 10% dei contagiati.
Work in Progress
Il modello descritto, pur semplificando notevolmente l’evoluzione temporale di un fenomeno molto complesso, consente il monitoraggio dell’effetto delle politiche intraprese e la previsione del loro impatto sia nel breve che nel medio/lungo periodo. Inoltre, l’approccio adottato offre una naturale estensione del modello nelle seguenti direzioni:
- Il modello può essere calibrato sulle diverse regioni italiane consentendo di tenere in considerazione l’eterogeneità dei parametri e di valutare politiche di contenimento più adeguate al contesto locale;
- Essendo basato su parametri con un chiaro significato epidemiologico, il modello può essere integrato con valutazioni di esperti o con evidenze derivanti da altri studi attraverso la definizione di distribuzioni a priori informative;
- Una volta elicitate delle distribuzioni di probabilità a priori sui parametri, questo metodo consentirà di derivare delle distribuzioni a posteriori sui parametri stessi e quindi una valutazione dell’incertezza sulle previsioni.
Riferimenti Bibliografici
Lin F., Muthuraman, K., Lawley M. (2010). An optimal control theory approach to non-pharmaceutical interventions. BMC infectious diseases. 10, article 32.

